 |
| A. tricoccum in local woods. |
Over-harvesting of A. tricoccum has led to the species disappearing from many areas where they used to be common. The plants grow very slowly, taking several years to grow from seed to a mature plant. The plants are also sensitive to physical disruption because their fragile roots grow close to the surface. If all the plants in an area are pulled out (or accidentally killed), then it could be decades before some seeds find their way back and start towards reestablishing a population.
At this time of year, the local foraging groups are filled with people posting pictures of their (often outrageous) harvests as well as people responding with ideas about sustainable practices of harvest. Advice to, "take no more than half" or, "only take 10%" are pretty common. There doesn't seem to be any standard number. I think some mathematical analysis can maybe help clarify what might be a good rule.
[1] Lets start with a very simple model. We have a population of plants and a whole bunch of people interested in harvesting them.
If everyone harvests 1/2 of the plants...
\(\lim \limits_{n\to\infty} \frac{1}{2}^n = 0\)
\(\lim \limits_{n\to\infty} \frac{3}{4}^n = 0\)
...then the population still dwindles towards extinction.
In this simplified model it doesn't matter what fraction each person takes, the population will always dwindle away towards extinction. This isn't realistic, since we didn't factor in the ability of the plants to reproduce.
[2] A slightly more complicated (and realistic) model factors in how fast the plant is able to replicate itself. Lets assume a fraction of of the adult plants are able to produce another adult plant each year. This is still a pretty big simplifying (and highly optimistic, since it is quite biologically wrong) assumption, but it's a starting point to work from. Lets start by defining some terms.
\(\begin{array}{cl}
R_y & \text{Population of Ramps in year 'y'.} \\
r_i & \text{Total increase rate per year.} \\
r_h & \text{Total harvest rate per year.} \\
\end{array}\)
R_y & \text{Population of Ramps in year 'y'.} \\
r_i & \text{Total increase rate per year.} \\
r_h & \text{Total harvest rate per year.} \\
\end{array}\)
The population of next year is calculated from the current year population and the total rate of increase.
\(R_y(1+r_i) = R_{y+1} \)
Then we add in a term for losses due to people harvesting a percentage of the plants.
\(R_y(1+r_i)(1-r_h) = R_{y+1} \)
If we want the population to remain stable over time...
\(R_y = R_{y+1} \)
\(R_y(1+r_i)(1-r_h) = R_{y+1} \)
\((1+r_i)(1-r_h) = \frac{R_{y+1}}{R_y} \)
\((1+r_i)(1-r_h) = 1 \)
\(1-r_h = \frac{1}{1+r_i} \)
\(r_h = 1-\frac{1}{1+r_i} \)
\(R_y(1+r_i)(1-r_h) = R_{y+1} \)
\((1+r_i)(1-r_h) = \frac{R_{y+1}}{R_y} \)
\((1+r_i)(1-r_h) = 1 \)
\(1-r_h = \frac{1}{1+r_i} \)
\(r_h = 1-\frac{1}{1+r_i} \)
...and we assume a third of the plants produce a second plant each year,
\(r_i = \frac{1}{3}\)
\(r_h = 1-\frac{1}{1+\frac{1}{3}} \)
\(r_h = 1-\frac{1}{\frac{4}{3}} \)
\(r_h = 1-\frac{3}{4} \)
\(r_h = \frac{1}{4} \)
\(r_h = 1-\frac{1}{1+\frac{1}{3}} \)
\(r_h = 1-\frac{1}{\frac{4}{3}} \)
\(r_h = 1-\frac{3}{4} \)
\(r_h = \frac{1}{4} \)
...then a cumulative total of 25% of the plants could be harvested each year. If any more were harvested, then the population would be declining like in our first model.
Remember, this is the cumulative total harvest rate. This could be just one person harvesting Ramps, or it could be several people harvesting separately through the season. If two or more people come across the patch and decide to harvest some, then they would have to harvest less than the 25% we calculated and still have the population remain stable. We have to define some new terms...
\(\begin{array}{cl}
n & \text{Number of people harvesting in a year.} \\
r_{hi} & \text{Harvest rate per individual per year.} \\
\end{array}\)
n & \text{Number of people harvesting in a year.} \\
r_{hi} & \text{Harvest rate per individual per year.} \\
\end{array}\)
The relationship between the number of individuals harvesting and the cumulative total harvest rate is pretty simple.
\((1-r_{hi})^n = (1-r_h) \)
\(\begin{array}{c|c}
{n} & {r_{hi} = 1-\sqrt[n]{\frac{3}{4}}} \\
\hline \\
{1} & {r_{hi} = 1-\frac{3}{4}} = 0.25 \\
{2} & {r_{hi} = 1-\sqrt{\frac{3}{4}}} \approx 0.13397 \\
{3} & {r_{hi} = 1-\sqrt[3]{\frac{3}{4}}} \approx 0.09144 \\
{4} & {r_{hi} = 1-\sqrt[4]{\frac{3}{4}}} \approx 0.06940 \\
{5} & {r_{hi} = 1-\sqrt[5]{\frac{3}{4}}} \approx 0.05591 \\
{\vdots} & {\vdots} \\
{10} & {r_{hi} = 1-\sqrt[10]{\frac{3}{4}}} \approx 0.02836 \\
{\vdots} & {\vdots} \\
{100} & {r_{hi} = 1-\sqrt[100]{\frac{3}{4}}} \approx 0.00287 \\
\end{array}\)
\(\begin{array}{c|c}
{n} & {r_{hi} = 1-\sqrt[n]{\frac{3}{4}}} \\
\hline \\
{1} & {r_{hi} = 1-\frac{3}{4}} = 0.25 \\
{2} & {r_{hi} = 1-\sqrt{\frac{3}{4}}} \approx 0.13397 \\
{3} & {r_{hi} = 1-\sqrt[3]{\frac{3}{4}}} \approx 0.09144 \\
{4} & {r_{hi} = 1-\sqrt[4]{\frac{3}{4}}} \approx 0.06940 \\
{5} & {r_{hi} = 1-\sqrt[5]{\frac{3}{4}}} \approx 0.05591 \\
{\vdots} & {\vdots} \\
{10} & {r_{hi} = 1-\sqrt[10]{\frac{3}{4}}} \approx 0.02836 \\
{\vdots} & {\vdots} \\
{100} & {r_{hi} = 1-\sqrt[100]{\frac{3}{4}}} \approx 0.00287 \\
\end{array}\)
The main lesson we can take from this second model is the more people that have access to a patch of Ramps, the smaller the fraction each person can harvest for the population to remain sustainable.
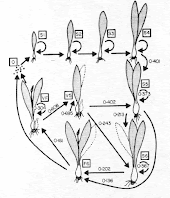 |
| From link. |
[3] Mathematically, a more ideal model would be somewhere between the discrete series function I used above and a set of continuous differential equations expressing the same concepts as well as accounting for stochasticity in the rates. Biologically, a more ideal model would include each life stage shown in the figure at right (encompassing sexual and vegetative reproduction) as well as realistic rates for each step.
It would be a relatively simple task to construct this sort of more detailed model, but properly determining all the rates would require extensive (presumably years-long) fieldwork. Thus, I'll leave this as an exercise for the reader.
Even though the models we discussed here are incomplete, they are informative. The big lesson is that the harvesting of Ramps from publicly accessible places is a nice example of a tragedy of the commons. There really isn't a harvesting percentage that can be used as a rule of thumb to tell people in the various forums.
If you have a large patch on your own land, then you can probably harvest a decent amount each year and the patch will never be at risk. Our hypothetical model [3] above might be able to tell us precisely how much of a population could be sustainably harvested, but without all the additional information it isn't worth worrying over. You can simply pay attention to how much you harvest and notice if the patch is dwindling or not from year to year. As it is your own patch, which you find valuable, you will adjust your personal harvest rate to allow the patch to prosper.
Is there anything we can encourage foragers to do, aside from simply advising them to leave the plants alone? If you harvest only one leaf from each mature plant (never the last leaf, or from small plants), without disturbing the bulb and roots, then the plants will survive and spread each year. If everyone followed this rule, large patches of Ramps could be maintained in woodlands close to or even within large cities. Convincing people to do this will be a difficult task.
References:
No comments:
Post a Comment